理解计算理论
什么能算,什么不能算?能算的话能需要多少空间和时间才能算出?这是关于计算的基本问题。虽然听来也许有点玄,但人们还是得到一些不仅美而且实在的结果。好像不存在通用压缩算法总能把文件压到比原来小,不然反复用它就能把文件压没了,这道理虽然浅显,但意味深长。
计算理论基于文本去建模,这决不是偶然的,而是基于文本在实践和理论上核心的地位:
- 计算机以致其它的计算装置与用户交互的媒介一般是文本,最终的输入和输出都主要通过文本呈现
- 文本本身也是通用的数据结构,文本处理是现代计算机最常见的计算
目前和可见将来的工程和物理条件决定了可靠的计算装置的上层必然是离散的,因此离散数学的结果和思维方式是从事计算机所应该具备的基本素质。其中,数学和编程最本质的概念都是递归,把问题分解从而化整为零。
文本的数学模型极其简单从而极其一般(其实数学甚至纯逻辑本身就要用符号串表达,文本应当比它们更根本,不过这里先不讨论元数学与数学的区别):
- 字符集在数学上不过看作一个有限集,其中元素称为字符
- 字符集$\Sigma$上的字符串集是指$\Sigma$上全体有限长度序列的集合$\Sigma^\ast =\bigcup^{\infty}_{i=0}\Sigma^i$,其中元素叫字符串
- 字符串集$\Sigma^\ast $的幂集称为字符集$\Sigma$上全语言类,其中的元素称为语言
计算理论的基本思想在于计算装置做的事实质上是判定一个任意字符串是否属于一个给定语言。于是为了把判断是非的问题就纳入了计算理论框架下,需要把输入集合对应到字符串集,把判断为是的输入的集合对应到一个语言。例如对于“判断一个有向图是否无环”的问题:
- 首先要对有向图编码(不必太完美),如令$\Sigma=\{0,1,x\}$为字符集,则就我们的目的可以为任意有向图中
- 每个顶点给一个不同的二进制编号
- 每条从编号$i$到编号$j$的边编码为$ixjx$
- 把所有边的编码串接起来作为整个图的编码
- 构造语言$L=\{w\in\Sigma^\ast \vert w\text{是一个有向无环图的编码}\}$
- 现在判断一个有向图$G$是否无环相当于判定$G$的其中一种编码是否属于$L$
即使看来不只是判断是非的问题,其实也常常可套用这框架,例如对于求“无向图中两个给定顶点间最短长度”的优化问题,它相当于一系列问题“最短长度二进制表示第i位是否1”。熟悉编码技巧的程序员应当已经相信这个框架足以容纳各种可想像的问题。
在研究计算理论时,需要建立计算装置的数学模型,不同的计算装置有不同的基本操作,对于每种计算装置模型,我们要问两个重要的问题:
- 最基本的问题是可计算性,即计算装置能和不能做什么。计算装置能解决一个问题是指,这装置能判定任一个串是否属于问题对应的某个语言。
- 其次是计算的复杂性,即计算所需的时间和空间资源。其中时间通常是通过基本操作步数衡量,空间则用使用过的存储单元数衡量。
本文主要参考John E. Hopcroft与Rajeev Motwani和Jeffrey D. Ullman的《自动机理论、语言和计算导论》和Michael Sipser的《计算理论导引》写成。
有限自动机与正则表达式
有限自动机是一种特别精简的计算装置模型,它只有有限的存储空间,它能判定的语言类是正则语言类。
正则表达式
给定字符集$\Sigma$,有基本的正则表达式:
∅是正则表达式,L(∅)=∅ϵ是正则表达式,L(ϵ)={()}- 若$a\in\Sigma$则
{a}为正则表达式,L(a)={(a)} 然后有一些操作用正则表达式构造更复杂的正则表达式: - 若
A、B为正则表达式,则(A|B)为正则表达式,L((A|B))=L(A)∪L(B) - 若
A、B为正则表达式,则(AB)为正则表达式,$L((AB))=\{(a_1,\cdots,a_m,b_1,\cdots,b_n)\vert (a_1,\cdots,a_m)\in A,(b_1,\cdots,b_n)\in B\}$ - 若
A为正则表达式,则(A*)为正则表达式,$L((A^\ast ))=\bigcup^{\infty}_{i=0}\{a_1\cdots a_i\vert a_j\in L(A)\}$ 其中L(A)称为正则表达式A对应的语言,我们把正则表达式对应的语言叫正则语言。
这样构造虽然不会有歧义,但括号太多了。显然,$((AB)C)$与$(A(BC))$匹配同一字符串类,所以不妨把它简记为$(ABC)$。类似地,$((A\vert B)\vert C)$匹配同一字符串类,所以不妨把它简记为$(A\vert B\vert C)$。再假定*、连接、$\vert$的优先级递减。这些规则可递归地应用,最后再可去掉暴露在最外面的括号对。如ab*匹配abbb但不匹配abab。
正则语言各运算的结合律、交换律、分配律、幂等律、零元、幺元等等比较明显,故不再具体写出。
现实中,在世界上已经存在上千种略有不同的“正则表达式”,它们在表示特殊字符的方法不全一样,还经常加入许多方便的缩写,甚至加入极少数实质性地增强表达能力的功能(如反向引用)。
有限状态机
有限自动机是对只有有限个状态的系统的抽象,从最简单的开关电路到最强大的计算机(内存依旧有限),很多协议也自然地用有限自动机表示。
确定型有限状态机
一个确定型有限状态机$A=(Q,\Sigma,\delta,q_0,F)$构成:
- $Q$是一个有限的集合,其中的元素叫状态
- $\Sigma$是有限的输入符号集
- $\delta : Q\times\Sigma\to Q$是转移函数
- $q_0\in Q$是初始状态
- $F\subseteq Q$是终结状态集
确定型有限状态机可以用图表直观地表示,为简便见一般省略一个死状态,所有没有标示的转移都进入这死状态。
每个确定型有限状态机接受一个语言,一个字符串$w=(a_0,a_1,\cdots,a_{n-1})$属于这个语言当且仅当这个向有限状态机输入它会导致机器进入一个接受状态,即令$q_i=\delta(q_{i-1},a_{i-1})$则$q_n\in F$。
给定$\Sigma$,容易构造接受以下以$\Sigma$为字符集的语言的自动机:
- 只有一个字符串的语言
- 所有长度为n的字符串组成的语言
- 所有长度为奇数(或偶数)的字符串组成的语言
用乘积自动机方法可构造接受两个分别由$(Q_1,\Sigma,\delta_1,q_{01},F_1)$、$(Q_2,\Sigma,\delta_2,q_{02},F_2)$接受语言之交语言的自动机$(Q_1\times Q_2,\Sigma,\{(((q_1,q_2),a),(\delta_1(q_1,a),\delta_2(q_2,a)))\vert q_1\in Q_1,q_2\in Q_2,a\in\Sigma\},(q_{01},q_{02}),F_1\times F_2)$。
非确定型有限状态机
非确定型有限状态机容许机器同时处于多个状态。形式上,把DFA定义中转移函数改为$\delta : Q\times\Sigma\to 2^Q$就成了NFA的定义。
每个非确定型有限状态机接受一个语言,一个字符串$w=(a_0,a_1,\cdots,a_{n-1})$属于这个语言当且仅当这个向有限状态机输入它会导致机器进入一个接受状态,即令$Q_0=\{q_0\}$、$Q_i=\bigcup_{q\in Q_{i-1}}\delta(q,a_{i-1})$则$Q_n\cap F\neq \emptyset$。
设计非确定型有限状态机有时比较容易,考虑接受所有包含(连续地或不一定连续地)一个给定子串的字符串组成的语言的自动机。
由于可以把一个状态集视为一个新的状态,非确定型有限状态机总可化为与之等价(接受相同语言)的确定型有限状态机。这说明一个重要的事实:一个语言被某个DFA接受当且仅当它被某个NFA接受。
我们总可以取状态集$Q$的幂集为对应NFA的状态集,这时它大小为$2^{\vert Q\vert }$,有时无可避免会达到这数量级(如考虑倒数第n个字符给定的语言,NFA用n+1个状态就够了,但DFA至少要$2^n$个状态,否则由抽屉原理必有两个长度为n的不同字符串可使DFA进入相同状态,再分别在它们后面加若干个相同字符则得到两个字符串倒数第n个字符不同却使用DFA进入相同状态,矛盾)。
非确定性机(不管是NFA还是后文的PDA与NTM)可以想像为在每步自我分裂一次。就如你买一次彩票并决定下次应买的n个彩票号,然后生n胞胎,再让你的孩子分别买这些彩票号,接着她们又生多胞胎去,如此类推,于是这家族吐气扬眉之时就是首度有人中彩票的一代。至少在目前看来,生产非确定性机在物理上是不可行的,我们讨论它们是因为它们在数学上往往较容易构造,且往往比对应确定性机步数少得多的特性使它们适合作为性能基准。
带ϵ转移非确定型有限状态机
非确定型有限状态机的一种推广是容许ϵ转移,即不消耗输入而转移状态。形式上,把DFA定义中转移函数改为$\delta : Q\times(\Sigma\cup\{\epsilon\})\to 2^Q$就成了ϵ-NFA的定义,其中$\epsilon\notin\Sigma$。一个状态q的ϵ闭包由所有从q开始仅通过ϵ转移可达的状态组成的状态集合,即各$closure(q)$为满足$q\in closure(q), closure(q)=\bigcup_{p\in\delta(q,\epsilon)}closure(p)$的最小集合。
每个ϵ-NFA也接受一个语言,一个字符串$w=(a_0,a_1,\cdots,a_{n-1})$属于这个语言当且仅当这个向有限状态机输入它会导致机器进入一个接受状态,即令$Q_0=closure(q_0)$、$Q_i=\bigcup_{q\in Q_{i-1}}closure(\delta(q,a_{i-1}))$则$Q_n\cap F\neq \emptyset$。
同样地,虽然构造ϵ-NFA有时比构造NFA方便,但ϵ-NFA都可转化为等价的DFA,转化方法也与从NFA到DFA的归约类似,把每个ϵ-NFA的状态对应到它的ϵ闭包。因此,一个语言被某个DFA接受当且仅当它被某个ϵ-NFA接受。
正则表达式与有限自动机的性质
正则表达式与有限自动机的能力
对于每个正则表达式,容易构造对应的ϵ-NFA接受它对应的语言。反之,DFA都可以化为正则表达式:
- 综合地看,可以归纳地构造正则表达式$R^k_{ij}$,它接受的语言为使状态从i只经前k个状态作为中间状态到达j的输入组成的集合:
- 当k=0,根本不能有中间状态,所以要么对应输入集合为$\{(\sigma)\vert \sigma\in\Sigma,\delta(i,\sigma)=j\}$,它显然可用正则表达式描述
- 假设小于k时已经完成构造,则可取$R^{k-1}_{ij}\vert (R^{k-1}_{ik}R^{k-1\ast}_{kk} R^{k-1}_{kj})$
- 最终$R^n_{1,n}$即为所求,其中1为初始状态而n为惟一接受状态(DFA总可等价化为只有一个接受状态的)和状态个数
当然在实用中构造$n^3$个正则表达式且长度每步增至约4倍不理想
- 分析地看可以逐步消除状态,仍设接受状态惟一:
- 开始时构造一个DFA与原来结构相同只是把字符换成正则表达式
- 对于各非初始或接受的状态s,对每对其它状态i和j,记从i到s的输入为I,从s到j的输入为J,从s到s的正则表达式为S,则把从i到j的输入R改为
R|IS*J,最后删除状态s - 若初始与接受状态相同(记为q),最后得到一个单状态DFA,从q到q的输入为R,这时$R^\ast $即为所求
- 若初始状态p与接受状态q不同,最后得到一个两状态DFA,记从i到j的输入为$R_{ij}$,这时$(R_{pp}^\ast \vert R_{pq}R_{qq}^\ast R_{qp})^\ast R_{pq}R_{qq}^\ast $即为所求
因此,一个语言为正则语言当且仅当它被某DFA(或NFA或ϵ-NFA)接受。
首先,我们看到正则语言类包含了很多有用的语言:
- 两个正则语言的交为正则语言(考虑乘积自动机)
- 两个正则语言的并、连接和星为正则语言(考虑正则表达式)
- 正则语言的补是正则语言(只用对DFA接受状态集取补),从而两个正则语言的差为正则语言
- 正则语言L的反转($\{(a_0,\cdots,a_{n-1})\vert (a_{n-1},\cdots,a_{0})\in L\}$)是正则语言(对正则表达式归纳论证即可)
- 设h为从$\Sigma^\ast $上的自同态(即$h((a_0,\cdots,a_{n-1}))=(h(a_0),\cdots,h(a_{n-1}))$),正则语言L的同态($h(L)$)是正则语言(对正则表达式替换就可看出)
- 设h为从$\Sigma^\ast $上的自同态,正则语言L的逆同态($h^{-1}(L)$)是正则语言(对DFA替换就可看出)
然而,我们也发现了许多描述起来很简单的语言并不是正则语言。一个简单的观察是泵引理:设L为一个正则语言,则存在正整数n使对任何长度大于等于n的A∈L,A可分解为BCD(其中$\vert C\vert >0,\vert BC\vert \leq n$)使对所有非负整数k,$BC^kD\in L$。这是因为取n为L对应DFA的状态数则从开始到接收n个字符期间经过n+1个状态,所以有两个不同时刻DFA处于相同状态,把这期间的输入记为C即可。利用泵引理,容易看出以下不是正则语言:
- $\{0^n1^n\vert n\text{为非负整数}\}$
- 由相同个数的0和1组成的字符串的集合
- 由素数个0组成的字符串的集合
本质上看根源在于有限自动机只能记住有限的信息。
正则表达式与有限自动机的判定问题
把n状态的NFA或ϵ-NFA转化为DFA需要$O(n^32^n)$时间。 把n状态的ϵ-NFA转化为NFA需要$O(n^3)$时间。 把n状态的DFA、NFA或ϵ-NFA转化为正则表达式需要$O(n^34^n)$时间。 把长度n的正则表达式转化为2n状态的ϵ-NFA需要$O(n)$时间。
为了判断一个正则表达式对应的语言是否为空,可以归纳地:
∅对应空语言ϵ对应非空语言- 若$a\in\Sigma$则
{a}对应非空语言 - 若
A、B为正则表达式,则(A|B)对应空语言当且仅当A和B都对应空语言 - 若
A、B为正则表达式,则(AB)对应空语言当且仅当A或B都对应空语言 - 若
A为正则表达式,则(A*)对应非空语言
给定一个DFA,为了判断一个长度n的串是否被接受,需要$O(n)$时间。给定一个有s个状态的NFA或ϵ-NFA,通过模拟运行判断一个长度n的串是否被接受,需要$O(ns^2)$时间。给定一个长度为s的正则表达式,由于可在$O(s)$时间内转化为约2s个状态的ϵ-NFA,故判断一个长度n的串是否被接受,需要$O(ns^2)$时间。
给定DFA的两个状态p、q,若对所有字符串$w\in\Sigma^\ast $,$\hat{\delta(p,w)}\in F$当且仅当$\hat{\delta(q,w)}\in F$,则称p、q等价(这确实是等价关系),否则称为可区分的。为了找出可区分的状态:
- 若p为接受状态而q不是,则p、q可区分
- 若$\delta(p,a)$与$\delta(q,a)$可区分则p、q可区分
不难看出没有被上述过程判定为可区分的状态对都是等价的。假定字符集大小为常数,则对于n状态的DFA,找出所有等价状态对需要时间不超过$O(n^4)$,实际上可取到最优的$O(n^2)$,方法是初始化依赖列表。现在为了判断两个DFA是否相同,作一个并DFA,然后判断两个原来的初始状态是否等价。这顺带给出判定两个正则表达式是否对应相同语言的方法。
正则表达式与有限自动机的应用
- 文本搜索。因为包含一个给定子串的字符串组成的语言可以由某NFA接受,所以可以自动化地构造,这给出了文本搜索的一种方法。当然文本搜索有其它方法,如倒排索引(用于搜索引擎,通过把开销转移到索引过程而使搜索几乎瞬间完成),但有限自动机胜在通用性,可进行正则表达式搜索,而且适应数据库实时变化的情况。
- 分词。在处理程序语言(包括各种基于文本的数据格式)时,通常会先把文本分成称为单词的单位。中文搜索同样依赖于分词。已经有程序可以自动生成分词器,如只用给出各类单词满足的正则表达式,Unix的lex或flex就可生成分词器的C程序,这比手工编写的分语工具容易维护。
另外,有限自动机也是电路设计、通信协议设计、用户界面设计等等的重要工具,在需要可靠性或安全性时特别适合。
有限自动机的最小化
在一个DFA经常被使用时,寻找一个与之等价但状态数最小的可以节省空间。当然,可以先删除所有不可达状态,然后DFA最小化的基本想法就是不断消除等价状态,最终得到的状态集由原来可达状态的等价类组成。
实际上,用上述方法得到的极小DFA就是最小的,并且等价的极小DFA是相互同构的。因为如果有等价的两个状态数不同的极小DFA,记为M、N,则它们的初始状态不可区分,而两个不可区分状态的后继也是不可区分的,所以对于M中每个状态p,用把M从初始状态带到p的输入把N带到q,于是p、q等价,这构造了从M的状态集到N的状态集的单射,所以M的状态数小于等于N的状态数,同理N的状态数小于等于M的状态数。
下推自动机与上下文无关语言
下推自动机是一种比有限自动机更为强大的计算装置模型,它有一个空间无界的栈,它能判定的语言类是上下文无关语言。
上下文无关语法
上下文无关语法(CFG)$G=(V,T,P,S)$的组成如下:
- 有限集V中元素称为非终结符
- 有限集T中元素称为终结符
- 有限集P中元素称为产生式,每个产生式形如$h\to c_1\cdots c_n$:
- $h\in V$为头
- $c_1\cdots c_n\in(V\cup T)^\ast $为体
- $S\in V$称为初始符号
给定一个CFG,把串中一个产生式的头换成其体的过程称为一步推导,若有产生式$h\to c_1\cdots c_n$,则对$a_1\cdots a_r hb_1\cdots b_s\in(V\cup T)^\ast $,有$a_1\cdots a_r hb_1\cdots b_s\Rightarrow a_1\cdots a_r c_1\cdots c_nb_1\cdots b_s$。接连进行零次或多次一步推导的过程叫推导,若有$A_0\Rightarrow A_1,\cdots,A_{k-1}\Rightarrow A_k$,则记$A_0\Rightarrow^\ast A_k$。CFG对应的语言$\{W\in(V\cup T)^\ast \vert S\Rightarrow^\ast W\}$称为上下文无关语言(CFL)。
从一串推导出另一个串可能有多种途径,最左推导过程中总是替换首个非终结符,最右推导过程中总是替换最后一个非终结符。任何到终结符串的推导都有等价的最左推导和最右推导(通过遍历语法树就可看出,进一步,它有两个不同语法树当且仅当它有两个不同的最左推导)。
推导可以用语法树表示,它的内部结点为非终结符,每个内部结点的各孩子结点依次为一个对应产生式的体的各符号(体没有符号则用特殊叶结点ϵ作为惟一孩子)。如果一个推导有不同的语法树,则称文法是有歧义的,例如:
- 在处理表达式时,可能写出产生式$E\to 1$、$E\to E \ast E$和$E\to E + E$,于是推导$E\Rightarrow E \ast E\Rightarrow E+E\ast E$和$E\Rightarrow E + E\Rightarrow E+E\ast E$对应的语法树不同。如果分别按两棵语法树求值,结果可能不同(前者把
+优先级视为高于*,后者相反)。为了避免这种歧义,比如我们把+的优先级视为低于*且假定它们左结合,则可以把上述产生式改为$E\to E + F$、$E\to F$、$F\to 1 \ast 1$和$F\to 1$。 - 在处理条件语句时,可能写出产生式$E\to S$、$E\to if ( B ) E$和$E\to if ( B ) E else E$,于是推导$E\Rightarrow if ( B ) E else E\Rightarrow if ( B ) if ( B ) E else E$和$E\Rightarrow if ( B ) E\Rightarrow if ( B ) if ( B ) E else E$对应的语法树不同。如果分别按两棵语法树求值,结果可能不同。为了避免这种歧义,比如我们按习惯让else与最后一个未配对的if对应(悬挂else),则可以把上述产生式改为$E\to if ( B ) E$、$F\to S$、$E\to F$和$F\to if ( B ) F else E$。
然而存在一些CFL的所有CFG都是歧义的,这样的CFL称为固有歧义的,如:
- $\{a^nb^nc^md^m\vert m,n\text{为正整数}\}\cup\{a^nb^mc^md^n\vert m,n\text{为正整数}\}$
乔姆斯基范式
应当指出,上下文无关语法中,即使进一步限制所有产生式形如以下之一:
- $A\to BC$,其中B、C都是非终结符
- $A\to a$,其中a是终结符
- $S\to \epsilon$,其中S是开始符号
并且不存在在所有推导都不出现的符号(无用符号),仍然足以刻画一切上下文无关语言,这样的语法叫乔姆斯基范式。要把一般的上下文无关语法化为这形式,可以:
- 去除无用符号,这实质上只用一次图遍历
- 上移ϵ产生式,方法是
- 找出所有可推导出空串的非终结符
- 删去所有ϵ产生式
- 对每个体中出现k次上述符号的产生式,换成$2^k$条产生式,分别由删除部分目标而成
- 若开始符号为上述符号,为它加上ϵ产生式
- 去除单位产生式
- 找出所有非终结符对$(A,B)$使$A\Rightarrow^\ast B$
- 去除所有单位产生式
- 对于每个上述的对$(A,B)$,对B的每个产生式增加一个体相同但头为A的产生式
- 分解长产生式,方法是把每个产生式$A\to B_1\cdots B_k(k>2)$换成k-1条产生式$A\to B_1A_1,A_1\to B_2 A_2 ,\cdots A_{k-2}\to B_{k-1}B_k$
- 去除体长度2产生式体中的终结符
- $A\to bC$换成$A\to BC$和$B\to b$
- $A\to Bc$换成$A\to BC$和$C\to c$
- $A\to bc$换成$A\to BC$、$B\to b$和$C\to c$
下推自动机
下推自动机(PDA)就是附上一个栈的ϵ-NFA,从而可以后进先出地记住任意有限长度的信息。形式地,$P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$构成:
- $Q$是一个有限的集合,其中的元素叫状态
- $\Sigma$是有限的输入符号集
- $\Gamma$是有限的堆栈符号集
- $\delta : Q\times(\Sigma\cup\{\epsilon\})\times\Gamma\to 2^{Q\times(\Gamma\times\Gamma\cup\Gamma\cup\{\epsilon\})}$是转移函数
- $q_0\in Q$是初始状态
- $Z_0\in \Gamma$是初始堆栈符号
- $F\subseteq Q$是终结状态集
PDA的一个瞬时格局由状态、剩余输入串和堆栈串组成,记为$(q,w,\gamma)$。若$(p,\alpha)\in\delta(q,a,X)$,则记$(q,aw,X\beta)\vdash(p,w,\alpha\beta)$,表示后者可由前者导出。一般地,$I_0\vdash I_1,\cdots,I_{k-1}\vdash I_k$,则记$I_0\vdash^\ast I_k$。注意到PDA从来看不到的数据不会影响它的计算:
- 若一个瞬时格局序列合法,则把同样的串加到各剩余输入串后得到的序列仍然合法
- 若一个瞬时格局序列合法,则把同样的串加到堆栈底部后得到的序列仍然合法
- 若一个瞬时格局序列合法,则把同样的未使用串从各剩余输入串后面删除后得到的序列仍然合法
PDA接受的语言有多种定义方法:
- 按终结状态方式定义为$L(P)=\{w\vert (q_0,w,Z_0)\vdash^\ast (q,\epsilon,Z),q\in F\}$。
- 按空栈方式定义为$N(P)=\{w\vert (q_0,w,Z_0)\vdash^\ast (q,\epsilon,\epsilon)\}$。
实际上,$\{L(P)\vert P\text{为}PDA\}=\{N(P)\vert P\text{为}PDA\}$,因为:
- 对于以终结状态结束的PDA,可以加上从终结状态到一个新状态的ϵ转移(对所有栈顶符号),进入这状态后会不断进行弹出操作(即这状态对所有栈顶符号有到自身的ϵ转移)。
- 对于以空栈结束的PDA,可以让开始时在栈底放一个特殊符号,以后一旦碰到它(不管在哪个状态)就ϵ转移到终结状态。
确定性下推自动机
设$P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$为一个PDA,如果:
- 对所有q、a、X,$\vert \delta(q,a,X)\vert \leq 1$
- 若有$a\in\Sigma$使$\delta(q,a,X)\neq\emptyset$则$\delta(q,\epsilon,X)=\emptyset$ 则称P为一个确定型下推自动机(DPDA)。
对于DPDA,以空栈结束的仍然可改成等价的DPDA以终结状态结束并接受相同语言,但反过来是不行的。易见,一个DPDA以终结状态接受的语言,在且只有在它有前缀性质(没有一个串是另一串的真前缀)时才能由某个DPDA以空栈接受。注意到正则语言$\{0\}^\ast $没有前缀性质,所以DPDA两种方式接受的语言类不同。这也不算大问题,因为在输入后加上终结符的话总是有前缀性质的。
上下文无关语言的性质
上下文无关语言的能力
给定一个CFG$G=(V,T,P,S)$,可以构造一个PDA$P=(\{q\},T,V\cup T,\delta,q,S,\emptyset)$,其中对每个非终结符A有$\delta(q,\epsilon,A)=\{(q,\beta)\vert A\to\beta\text{为}G\text{的产生式}\}$,对每个终结符a有$\delta(q,a,a)=\{(q,\epsilon)\}$,这PDA本质上不断在找最左推导,故有$L(G)=N(P)$。
反之,给定一个PDA$P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$,可以构造一个CFG$G=(\{S\}\cup Q\times\Gamma\times Q,\Sigma,R,S)$,其中$R=\{S\to q_0Z_0p\vert p\in Q\}\cup\{qXr_k\to a(rY_1r_1)(r_1Y_2r_2)\cdots(r_{k-1}Y_kr_k)\vert (r,Y_1\cdots Y_k)\in\delta(q,a,X)\}$,其中非终结符$pXq$的含义是从状态p的情况转移到状态q并弹出栈顶符号X过程中接受的字符串,故有$L(G)=N(P)$。
这说明一个语言为上下文无关语言当且仅当它被某PDA(以空栈或终结状态方式)接受。
由于DPDA可当作DFA用,正则语言都可用某DPDA以终结状态接受,而且有的可以被DPDA接受(两种方式都有)的语言不是正则语言,如$\{0^n1^n\vert n\text{为正整数}\}$。能被DPDA接受的语言自然可由某PDA接受,反之不然,如回文语言$\{a_1\cdots a_na_n\cdots a_1\vert n\text{为非负整数},a_i\in\{0,1\}\}$显然是上下文无关语言,但没有DPDA刚好接受它(直观上,如果DPDA在发现$0^n110^n$时势必把栈清空,于是它无力判断$0^n110^n0^m110^m$是否回文)。事实上,DPDA接受(不管以空栈还是终结状态)的语言都是非固有歧义的,从接受过程可知最左推导惟一。
现在看看CFL的能力,从正面说,它有一些封闭性:
- 两个CFL的并为CFL
- 两个CFL的连接为CFL
- CFL的星为CFL
- CFL的反转为CFL
- CFL的同态为CFL
- CFL的逆同态为CFL
- CFL与正则语言的交为CFL
其中前四项用CFG的观点看是明显的,而后三项用PDA看比较容易。
最后我们证明存在非上下文无关的语言,相应地我们建立一个泵引理:若L为一个CFL,则存在n使对任何L中长度不小于n的串z,有z=uvwxy使$\vert vwx\vert \leq n,\vert vx\vert >0$且对任何非负整数i,$uv^iwx^iy \in L$。事实上取$n=2^m$,其中m为乔姆斯基范式中符号数,于是在z的语法树中至少有一条路径长m+1(否则叶子数到不了n),从而其中有两个结点对应相同的非终结符(不妨设它们是最低的两个),让它们分别对应输入vwx和w即知结论成立。
利用泵引理,容易看出以下语言不是CFL:
- $\{0^i1^j2^i3^j\vert i,j\text{为正整数}\}$
- $\{ww\vert w\in\{0,1\}^\ast \}$(考虑$0^m1^m0^m1^m$)
但$\{0^i1^j2^i3^j\vert i,j\text{为正整数}\}=\{0^i1^j2^i3^k\vert i,j,k\text{为正整数}\}\cap\{0^i1^j2^k3^j\vert i,j,k\text{为正整数}\}$,这表明CFL对交是不封闭的,从而对补和差也不封闭。
上下文无关语法的判定问题
把长度为n的CFG转换为对应长度$O(n)$PDA需要$O(n)$时间。反之,把长度为n的PDA转换为对应长度$O(n^3)$CFG需要$O(n^3)$时间。
要判定CFG是否给出空语言,先把所有终结符和ϵ产生式的头标记为非空的,然后每当发现有产生式体的所有分量已标记为非空,则把目标也标记为非空,最后看开始符号有否标记为非空。假设CFG长度为n,这可在$O(n)$时间完成(通过构造依赖列表)。
要判断一个长度n的串是否属于一个由乔姆斯基范式给出的CFL,可以用动态规划的思想,构造一个表格中表项$V_{ij}$表示从第i个字符到第j个字符组成的子串可从哪些非终结符推导出,这表可以按$j-i$递增顺序构造,最后检查开始符号是否在$V_{0,n}$中,或者n=0但S有ϵ产生式。这过程可以在$O(n^3)$时间内完成。
能从初始符号推导出的叫句型,其中用最左(右)推导可得的称为左(右)句型。
最后,我们列出一些不可判定的问题:
- 一个CFG是否歧义的
- 一个CFL是否固有歧义的
- 两个CFL的交是否为空
- 两个CFL是否相同
- 一个CFL是否等于$\Sigma^\ast $,其中$\Sigma$为该语言的字符集
应用
大多数编程语言和数据语言的语法都用上下文无关语法描述,只要把语法和对应动作写好,yacc和bison之类就能自动生成解析器C程序。
对于应用来说,解析一般上下文无关语言的复杂度可能还不让人满意,所以人们构造的语言往往属于更限制性的语言类,对于这些语言类,存在线性时间的解析算法,相应的限制通常是只用向前看k个终结符(而且常取k=1):
- $LL(k)$寻找最左推导
- $LR(k)$寻找最右推导
对于每个$k$,可以证明$LL(k)\subset LR(k)$。它们的原理并不困难,请参考编译原理的材料。
对于XML之类的元语言,也有DTD和Schema之类描述具体的语言。
图灵机
图灵机的定义
图灵机(TM)基本上为附上可数无穷存储空间的有限状态机,可想像成有一条分成无穷多个格子的纸带,一个读写头附在其中一格上,它根据格子中记号和自身状态决定一步行动,即把状态和当前格子中记号改成什么,以及读写头向哪个方向移动一格(或者停机)。形式上说,图灵机$M=(Q,\Sigma,\Gamma,\delta,q_0,B,F)$的组成如下:
- $Q$为有限的状态集合
- $\Sigma\subseteq\Gamma$为输入符号的有限集合
- $\Gamma$是带符号集合
- $\delta:Q\times\Gamma\to Q\times\Gamma\times\{L,R,S\}$是转移函数
- $q_0\in Q$是开始状态
- $B\in\Gamma\setminus\Sigma$是空格符号,可以想像开始时没有放输入的格子都是空格
- $F\subseteq Q$是接受状态集
为方便见,用$X_1\cdots X_{i-1}qX_iX_{i+1}\cdots X_n$描述TM的瞬时格局,它表示TM处于状态q,当前带符号为$X_{i}$,而带上左方的符号依次为$X_{i-1},\cdots,X_1$,带上右方的符号依次为$X_{i+1},\cdots,X_n$,余下格子中符号全为空格$B$。给定TM和TM的瞬时格局,则可以导出它的下一个瞬时格局:
- 若$\delta(q,X_i)=(r,Y,L)$,则$X_1\cdots X_{i-1}qX_iX_{i+1}\cdots X_n\vdash_M X_1\cdots pX_{i-1}YX_{i+1}\cdots X_n$(i>1)或者$qX_1\cdots X_n\vdash_M X_1\cdots pBYX_2\cdots X_n$
- 若$\delta(q,X_i)=(r,Y,R)$,则$X_1\cdots X_{i-1}qX_iX_{i+1}\cdots X_n\vdash_M X_1\cdots X_{i-1}YpX_{i+1}\cdots X_n$(i<n)或者$X_1\cdots X_{n-1}qX_n\vdash_M X_1\cdots X_1\cdots X_{n-1}YpB$
- 若$\delta(q,X_i)=(r,Y,S)$,则TM停机
若$\alpha_0\vdash_M \alpha_1,\cdots,\alpha_{k-1}\vdash_M \alpha_k$则记$\alpha_0\vdash^\ast _M \alpha_k$。这样TM接受的语言为$\{w\in\Sigma^\ast \vert q_0w\vdash^\ast _M\alpha q\beta,q\in F\}$。能被某TM接受的语言称为递归可枚举语言。
“递归可枚举语言”这名字来源于有枚举器可枚举它,所谓枚举器是指一个带打印机的图灵机,它会且只会打印语言中的串。这两种定义方式是等价的:
- 若有一个TM接受一个语言,则对每个非负整数$i$,对前$i$个可能串分别模拟运行原TM$i$步,若进入接受状态则打印对应串
- 若有一个语言的枚举器,则可构造一个TM模拟这枚举器,它当打印出与输入串相同的串时进入状态
我们约定进入接受状态时图灵机总是停机(即使让它继续对我们也没有影响),从而对于接受的串TM总是会停机,但如果一个串不被接受,则TM可能停在非接受状态或者永远不停机。对所有输入都停机的图灵机称为算法。能被某算法接受的语言称为递归语言。
上面只用到停机时的状态,但带上的内容有时也是有用的。设$f:\Sigma^\ast \to\Sigma^\ast $,若存在算法M使对所有输入$w\in\Sigma$,停机时带上除去两端空白外只有$f(w)$,则称$f$是可计算函数。
图灵机的变种
图灵机可以进行多种扩展或限制,但仍然有相同的计算能力。
- 多带图灵机有多条纸带和多个读写头,初始时所有输入放在第一条带上,读写头在其左侧(其它带初始位置无所谓),然后按当前状态和各带当前符号决定当前状态和各带当前符号改成什么,还有各读写头各自向什么方向移动或不动。 为了用单带图灵机模拟多带图灵机,让单带符号$(A_1,X_1,\cdots,A_k,X_k)$中$A_i$表示多带机的第i条带对应位置的带符号而$X_i$表示多带机的第i条带对应位置的是否读写头的当前位置,这样把带符号赋予有用结构的方法叫多道。代价是用单带机模拟多带机的n步需要$O(n^2)$步(因为在n步后各读写头的距离不超过2n)
- 非确定性图灵机对每个状态和带符号给出零个或多个可选的转移,一个串被接受当且仅当存在一系列转移选择可达到接受状态。 模拟方法是依次找出非确定性图灵机在若干步内可到达的瞬时格局集合(广度优先搜索),直到发现接受状态。代价是这样用确定性图灵机模拟非确定性图灵机的n步需要$O((nm^n)^2)$步,其中m为每步最多可选的转移数。
- 带半无穷带且不写空格的图灵机 要实现不写空格,只用引入一个作用类似空格的新带符号;要禁止读写头移到初始位置的左方,只用把双向带布局$\cdots X_{-1}X_0X_1\cdots$对应于单向带布局$BX_0X_{-1}X_1\cdots$
- 有随机访问能力的图灵机
- 有多于一个堆栈的下推自动机
- 有多于一个计数器代替堆栈的下推自动机
现代的电子计算机的能力甚至没有达到图灵机(因为存储空间有限),用图灵机模拟计算机并不困难(用多带图灵机更方便,让存储器、程序计数器、当前存储地址和草稿用不同带,其中存储器格局为地址、内容和分隔符),虽然计算机n步可能对应到图灵机$O(n^6)$步。丘奇论题推测,任何可想像的计算装置的计算能力都不超出图灵机。对此,有一些哲学上的论证。
不可判定性
基本概念
注意到问题(即语言)有不可数无穷多个,但图灵机只有至多可数无穷多个,所以必定存在不可判定(非递归)的问题,实际上几乎所有问题都是不可判定的。几乎所有问题都不能算的事实曾经让人相当吃惊,与之对应的是数理逻辑中的哥德尔不完备性定理。
最明显的一个不可判定的问题是停机问题,即没有总是停机的图灵机可判定任意给定的图灵机(不难编码它)和输入串是否最终会进入停机状态,因为如果有这样的图灵机M,可以构造一台图灵机用M判定自身会否最终终止,如果得知是则进入死循环,否则马上终止,这就导出了矛盾。
实际上,有更强的结论,有根本不存在TM接受的语言。为此用对角线证法,首先对所有串和图灵机分别用正整数编号,然后构造表格$(a_{ij})^\infty_{i,j=1}$,其中第i行第j列为1当且仅当第i个图灵机接受第j个串(否则为0),这样对角线的补$(1-a_jj)^\infty_{j=1}$与任一行$(a_{ij})^\infty_{j=1}$都不同,所以对应语言$\{\text{串}j\vert 1-a_{jj}=1\}$不能由任何图灵机接受。
易见,递归语言的补是递归语言(对TM的接受状态集取补即可)。假如一个语言和其补都是递归可枚举的,则实际上它们都是递归的(可以构造一台TM交错地模拟两台TM,这样两台原TM恰有一台最终进入接受状态,若为前者则新TM进入接受状态,否则进入拒绝状态)。注意到停机问题是递归可枚举的(可以模拟运行输入的图灵机),所以,递归可枚举语言不一定为递归语言。顺带知停机问题的补不是递归可枚举的。
证明一个语言非递归或非递归可枚举的通常策略是归结:若存在算法,它以语言A的串为输入在停机时得到非B的串,它以非语言A的串为输入在停机时得到非语言B的串,则称语言A可归结到语言B。若语言A可归结到语言B,则A非递归时B也非递归,A非递归可枚举时B也非递归可枚举。
作为例子,考虑由所有接受语言非空的图灵机组成的语言,它显然是递归可枚举的(因为容易构造非确定性图灵机来检验所有可能输入),又因停机问题可归约到它(让停机时的状态总是接受状态),故它不是递归的,因而所有接受空语言的图灵机组成的语言不是递归可枚举的。
实际上,递归可枚举语言的任何非平凡性质(递归可枚举语言的集合的非空真子集)都是不可判定的,因为停机问题可归约到它(若空语言不属于性质,对任何图灵机M和输入w,构造图灵机$M’$它模拟用w运行M,接受的话再以自身输入运行判定L的图灵机,于是$M’$接受空语言当且仅当$(M,w)$不停机;若空语言属于性质,则由上补性质不可判定,于是原性质也不可判定)。特别地,以下问题都是不可判定的:
- 一个TM接受的语言是否有限的
- 一个TM接受的语言是否正则语言
- 一个TM接受的语言是否上下文无关语言
相应地,与程序做什么有关的任何非平凡问题都是不可判定的。这完全是合理的,如果静态分析如此强大,根本不用运行程序。
波斯特对应问题
前面介绍的不可判定问题比较做作,下面讨论的波斯特对应问题没有涉及到图灵机。
给定串$w_1,\cdots,w_k,x_1,\cdots,x_k\in\Sigma^\ast $,则对应PCP问题考虑$\{w_{i_1}\cdots w_{i_j}\vert w_{i_1}\cdots w_{i_j}=x_{i_1}\cdots x_{i_j}\}$是否非空。
PCP的变种MPCP考虑$\{w_1w_{i_1}\cdots w_{i_j}\vert w_1w_{i_1}\cdots w_{i_j}=x_1x_{i_1}\cdots x_{i_j}\}$是否非空。我们把停机问题归约到MPCP,给定图灵机$M=(Q,\Sigma,\Gamma,\delta,q_0,B,F)$和输入$w\in\Sigma^\ast $,取$\#\notin \Gamma\cup Q$,如下构造MPCP:
| w | x | 备注 |
|---|---|---|
| $\#$ | $\#q_0w\#$ | |
| $X$ | $X$ | 对$\Gamma$中每个$X$ |
| $\#$ | $\#$ | |
| $qX$ | $Yp$ | 对$\delta(q,X)=(p,Y,R)$ |
| $ZqX$ | $pZY$ | 对$\delta(q,X)=(p,Y,L),Z\in\Gamma$ |
| $q\#$ | $Yp\#$ | 对$\delta(q,B)=(p,Y,R)$ |
| $Zq\#$ | $pZY\#$ | 对$\delta(q,B)=(p,Y,L),Z\in\Gamma$ |
| $XqY$ | $q$ | 对$q\in F, X,Y\in\Gamma$ |
| $Xq$ | $q$ | 对$q\in F, X\in\Gamma$ |
| $qY$ | $q$ | 对$q\in F, Y\in\Gamma$ |
| $q\#\#$ | $\#$ | 对$q\in F$ |
这PCP有解当且仅当$(M,w)$停机,实际上PCP的解与TM的瞬时格局序列对应,第一个串中瞬时格局一般领先第二个串中瞬时格局一步。
现在把MPCP归约到PCP,对于给定串$w_1,\cdots,w_k,x_1,\cdots,x_k\in\Sigma^\ast $,取$\#,\$ \notin\Sigma$,
- 对$i=1,\cdots,k$,令$y_i$由在$w_i$中每个字符后加$\#$而成,$z_i$由在$x_i$中每个字符前加$\#$而成
- 令$y_0=\#y_1, z_0=z_1,y_{k+1}=\$, z_{k+1}=\#\$$ 则$y_0,\cdots,y_{k+1},z_0,\cdots,z_{k+1}$为对应的PCP问题,易见这PCP的解必形如$y_0w_{i_1}\cdots y_{i_j}=z_0z_{i_1}\cdots z_{i_j}$,它对应MPCP的解$w_0w_{i_1}\cdots w_{i_j}=x_0x_{i_1}\cdots x_{i_j}$。
我们把波斯特对应问题归约到以下问题,从而说明它们不可判定,给定串$w_1,\cdots,w_k,x_1,\cdots,x_k\in\Sigma^\ast $:
- CFG的歧义性。构造上下文无关语法以S为开始符号,有产生式:
- $S\to A, S\to B$
- $A\to w_1Aa_1,\cdots,A\to w_kAa_k,A\to w_1a_1,\cdots,A\to w_ka_k$
- $B\to x_1Aa_1,\cdots,A\to x_kAa_k,B\to x_1a_1,\cdots,A\to x_ka_k$ 则这个PCP问题有解当且仅当这CFG有歧义
- 两个CFG给出语言之交是否为空。记$L_A,L_B$分别为上述A、B导出串组成的CFL,则PCP问题有解当且仅当$L_A\cap L_B\neq\emptyset$。
- 一个正则语言是否包含于一个CFG的语言。注意到上述$L_A$的补是上下文无关语言(可直接构造DPDA,在遇到a之前一直压入输入字符,之后开始检查)。现在有CFG$G$使$L(G)=L_A^C\cup L_B^C=(L_A\cap L_B)^C$,正则表达式R使$L(R)=(\Sigma\cup\{a_1,\cdots,a_k\})^\ast $,于是PCP问题无解当且仅当$L(G)=L(R)$(这相当于$L(R)\subset L(G)$)。
- 一个CFG和一个正则表达式是否对应相同语言。这是上一点说明的产物。
- 两个CFG是否给出相同语言。容易把上一问题归约到这问题。
- 一个CFG的语言是否包含于另一个CFG的语言。因为上一问题可轻易归约到这问题(相等即相互包含)。
- 两个TM是否给出相同语言。因为对于CFG可构造接受它的TM。
其实还有一些不涉及计算理论对象的不可判定问题:
- 一个整系数多元多项式是否有整数根(希尔伯特第10问题),虽然它是递归可枚举的,但不是递归的。作为一个推论,计算根的常见范数上界也是不可能有算法。
计算复杂度
基本概念
前面我们讨论了图灵机能做和不能做什么,但在现实中资源是有限的,我们仅仅知道用有限步和有限空间能解决问题并不够精确,我们还想知道究竟用了多少步和多少空间。
给定一个算法M,定义$T=\{(n,\max\{M\text{对输入}w\text{在停机前的转移数}\vert w\in\Sigma^\ast ,\vert w\vert \leq n\})\vert n\text{为非负整数}\}$为M的时间复杂度,定义$S=\{(n,\max\{M\text{对输入}w\text{在停机前擦写的空白数}\vert w\in\Sigma^\ast ,\vert w\vert \leq n\})\vert n\text{为非负整数}\}$为M的空间复杂度。显然,对所有n,$S(n)\leq T(n)$。
通常,人们认为复杂度不超过多项式为比较好的情况,虽然许多复杂度非多项式的算法也很有用。有不少人习惯把非多项式的都叫指数,但严格地说,$f:n\mapsto n^{\log n}$就是介于多项式函数与指数函数间的,而且比指数函数增长快的函数也多的是,所以我们不用这说法。选择多项式的一个原因是典型计算设备间模拟的步数是多项式的,不过,非典型的不知道,如时间复杂度$T$的非确定性算法总可以转换为时间复杂度$C^T$的确定性算法,但我们不知道有没有多项式的。
给定算法M,若存在多项式函数$P$使$T(n)=O(P(n))$,则称M为多项式时间算法或P算法;若存在多项式函数$P$使$S(n)=O(P(n))$,则称M为多项式空间算法或S算法。显然,P算法必为S算法,反之不然。
相应地,给定非确定性算法M(即一台图灵机,对任何输入都存在导致停机的转移序列),这时时间和空间复杂度定义中步数和格数理解为最短接受历史中步数和使用格数最少的接受历史使用的格数,若存在多项式函数$P$使$T(n)=O(P(n))$,则称M为非确定性多项式时间算法或NP算法;若存在多项式函数$P$使$S(n)=O(P(n))$,则称M为非确定性多项式空间算法或NS算法。显然,NP算法必为NS算法。
我们把所有存在P、NP、S、NS算法的语言类分别称为$\mathcal{P}$、$\mathcal{NP}$、$\mathcal{S}$、$\mathcal{NS}$问题类。显然,$\mathcal{P}\subseteq\mathcal{NP},\mathcal{S}\subseteq\mathcal{NS},\mathcal{P}\subseteq\mathcal{S},\mathcal{NP}\subseteq\mathcal{NS}$。
一个观察是若图灵机只用$p(n)$空间,则如它接受一个串,则在$(p(n)+1)\vert \Gamma\vert ^{p(n)}\vert Q\vert $步内已经接受(因瞬时格局数不超过它),所以使用多项式空间的图灵机总可改成接受相同语言的算法(模拟原TM有限步即可)。这结论对非确定性情况也成立。更有意思的是,$\mathcal{S}=\mathcal{NS}$,原因是可以先把NTM改成只有一个接受的瞬时格局,然后递归地计算从瞬时格局I在$2^m$步内达到瞬时格局J由于递归深度可控制在上述步数界的对数$O(p(n))$,而每个栈帧只用$O(p(n))$空间,所以确定性图灵机用$O(p(n)^2)$空间足以完成计算。
关于NP问题L,还有一种理解方式,就是存在多项式时间的验证机,验证机是一台多带图灵机,使$w\in L$当且仅当存在c使第两条带初始化为c时w被接受(多项式时间只是指w长度的多项式)。这两种理解方式是一致的:
- 给定NTM,可以让c对应于选择的转移序列
- 给定验证机,则可构造NTM猜测c
正如考虑不可判定性时要用归约,考虑复杂度时要用多项式归约。若存在从语言A到语言B的多项式归约算法(相应地,可计算函数),则称语言A可多项式归结(相应地,可映射归约)到语言B。若语言A可归结到语言B,则B为$\mathcal{P}$问题时A也是。
一个获得广泛关注的未解问题是,是否有$\mathcal{P}=\mathcal{NP}$?
NS完全问题
NS(S也一样)问题中最耗费时间(没打错)的问题称为NS完全问题。也就是说,它们组成的问题类$\mathcal{NSC}=\{L\in\mathcal{NS}\vert \text{所有NS问题可多项式归约到}L\}$。
- 如果有一个NS完全问题为P问题,则$\mathcal{NS}=\mathcal{P}$。
- 如果有一个NS完全问题为NP问题,则$\mathcal{NS}=\mathcal{NP}$。
我们举出一个NS完全问题的例子,即带量词布尔公式(QBF)。通过重命名变元不妨设带量词布尔公式的构成如下:
0、1和任何变元为QBF- 若
E、F为QBF,则(E)∧(F)、(E)∨(F)和¬(E)都是QBF - 若
E为不含对变元x量化的QBF,则∀x(E)和∃x(E)都是QBF
对于没有自由变元的QBF,容易递归地计算其值。QBF问题就问一个QBF的值是否为1。容易验证这问题是NS的,这只用从内而外化简,非量化的部分不用额外空间,量化也只用暂时复制一份子QBF。下面验证所有S问题都可以多项式归约到QBF问题,方法是用QBF问题刻画图灵机。给定输入$a_1\cdots a_n$和至多用$p(n)$空间的图灵机,对于每个瞬时格局,可用变元$x_{jA}(j=0,\cdots,p(n),A\in\Gamma)$表示第$j$个位置为$A$:
- 用变元$y_{jA}(j=0,\cdots,p(n),A\in\Gamma)$表示开始时瞬时格局Y,则图灵机正确开始相当于$S=y_{0q_0}\wedge y_{1a_1}\wedge\cdots\wedge y_{na_n}\wedge y_{n+1,B}\wedge\cdots\wedge y_{p(n),B}\wedge\wedge_{\text{其它}}\lnot y_{jA}$为1,这式子的构造显然可在多项式时间完成
- 用变元$z_{jA}(j=0,\cdots,p(n),A\in\Gamma)$表示结束时瞬时格局Z,则图灵机正确结束相当于$E=\bigvee^{p(n)}_{i=0}\bigvee_{X_j\in\Gamma,q\in F}z_{0X_0}\wedge\cdots\wedge z_{i-1,X_{i-1}}\wedge z_{iq}\wedge z_{i+1,X_{i+1}}\wedge\cdots\wedge z_{p(n),X_{p(n)}}$为1,这式子的构造显然可在多项式时间完成
- 现在归纳地构造表示在$2^k$步内可从瞬时格局I到瞬时格局J的公式$N_k(I,J)$
- 当k=0,把转移函数翻译过来就好了,这式子的构造显然可在多项式时间完成
- 当$k-1$情况已解决,则$N_k(I,J)=\exists K \forall P \forall Q(N_{k-1}(P,Q)\vee(\lnot(I=P\wedge K=Q)\wedge\lnot(K=P\wedge J=Q)))$(内部公式在说$(P,Q)=(I,K)\vee(P,Q)=(K,J))\to N(P,Q)$,于是整个在说$\exists K (N(I,K)\wedge N(K,J))$) 因为这图灵机若接受输入,必在$2^{Cp(n)}$步内接受,所以$N=N_{Cp(n)}(Y,Z)$表示图灵机能否从Y转移到Z
于是图灵机接受串当且仅当QBF$\exists Y\exists Z(S\wedge E\wedge N)$为1
QBF问题有一种有趣的解读,给定前束范式$\phi=\exists x_1\forall x_2\exists x_3\forall x_4\cdots\psi$,在一场博弈中两个选手轮流决定变元$x_1,x_2,\cdots$的值,若最后得$\psi$为真则前一选手胜,这样$\phi$可满足当且仅当前一选手有某种必胜策略。这说明判定这游戏中是否有必胜策略是一个NS完全问题。
NP完全问题
至少和任意NP完全问题一样难,即所有NP问题都可多项式归约到它的问题称为NP难问题(不必是NP的)。
我们把$\mathcal{NP}$问题类中的NP难问题称为NP完全问题,它们组成问题类$\mathcal{NPC}$。也就是说,NP问题是NP问题中最难的。特别地,任意两个NP完全问题可以相互多项式归约。如果一个NP完全问题可归约到一个NP问题,则后者也是NP完全的。由于$\mathcal{P}=\mathcal{NP}$当且仅当存在一个NP完全问题是P问题,所以NP完全问题处于特殊的地位。现在已经发现成千上万个NP完全问题,但没有一个被确定是否P问题。似乎多数人倾向认为$\mathcal{P}\neq\mathcal{NP}$,从而NP问题都是非多项式的,这给出了验证一个问题坏的方法,当然一切只是猜测。
接着,我们直接给出一个NP完全问题:布尔表达式的可满足性问题(SAT),即是否存在变元的某种取值(每个只能取0或1)可使之为真,其中布尔表达式由变元(用二进制编码)经与、或和否定构成。例如$x0\wedge x0$是不可满足的。SAT显然是NP的,因为用非确定性图灵机可以猜测所有可能取值。后面要证明所有NP问题可多项式归约到SAT,为此给定接受语言L的一个时间复杂度为多项式$p$的NP算法M,对于所有输入$w=a_1\cdots a_n$,我们要在多项式时间里构造一个布尔表达式模拟M,使M接受w当且仅当这布尔表达式可满足:
- 为表示我们关心的瞬时格局序列,引入布尔变元$y_{ijA}(i,j\in\{0,\cdots,p(n)\},A\in\Gamma\cup Q)$表示第$i$步后瞬时格局$\alpha_i$的第$j$位置$X_{ij}$为$A$。
- 为了保证上述表示的合法性,要求$U=\bigwedge^{p(n)}_{i,j=0}\bigwedge_{Y,Z\in\Gamma\cup Q,Y\neq Z}\lnot(y_{ijY}\wedge y_{ijZ})$
- 正确开始相当于$S=y_{00q_0}\wedge y_{01a_1}\wedge\cdots\wedge y_{0na_n}\wedge y_{0,n+1,B}\wedge\cdots\wedge y_{0,p(n),B}$
- 正确结束相当于$E=\bigvee_{q\in F}\bigvee^{p(n)}_{j=0}y_{p(n),j,q}$
- 每一步正确相当于每一步正确$N=N_{1}\wedge\cdots\wedge N_{p(n)}$,按原状态的位置再分解$N_i=\bigwedge^{p(n)}_{j=0}(A_{ij}\vee B_{ij})$
- $A_{ij}=\bigvee_{q,p\in Q,D,Y,Z\in\Gamma,\delta(q,Y)=(p,Z,L)}(y_{i-1,j-1,D}\wedge y_{i-1,j,q}\wedge y_{i-1,j+1,Y}\wedge y_{i,j-1,p}\wedge y_{i,j,D}\wedge y_{i,j+1,Z})\vee\bigvee_{q,p\in Q,D,Y,Z\in\Gamma,\delta(q,Y)=(p,Z,R)}(y_{i-1,j-1,D}\wedge y_{i-1,j,q}\wedge y_{i-1,j+1,Y}\wedge y_{i,j-1,D}\wedge y_{i,j,Z}\wedge y_{i,j+1,p})$
- $B_{ij}=\bigvee_{Z\in\Gamma}y_{i-1,j,Z}\wedge\bigvee_{Z\in\Gamma}(y_{i-1,j,Z}\wedge y_{ijZ})$
现在$S\wedge N\wedge E\wedge U$即为所要的。
以下继续把SAT多项式归约到其它问题,从而证明它们是NP完全问题。第一个问题还是逻辑的但看似更容易,余下的将是图论中的典型问题,最后是一个纯算术问题。
先讨论合取范式的可满足性问题(CSAT),其中合取范式形如$\bigwedge_{i\in I}\bigvee_{j\in J_i}X_{ij}$,其中$X_{ij}$为变元或其否定,所有$\vert J_i\vert =k$的合取范式叫k合取范式。虽然可把任意布尔公式化为合取范式,但这可能会使长度指数式增长。取而代之,先用德摩根律和双否定律使否定只出现在变元的直接前方,然后递归地化为有相同可满足性的合取公式:
- 对$E=E_1\wedge E_2$,把$E_1,E_2$分别化为合取范式$F_1,F_2$且它们变元集之交包含于$E$的变元集,则$F=F_1\wedge F_2$为合取范式,与$E$有相同的可满足性
- 对$E=E_1\vee E_2$,把$E_1,E_2$分别化为合取范式$F_1=g_1\wedge\cdots\wedge g_p,F_2=h_1\wedge\cdots\wedge h_q$且它们变元集之交包含于$E$的变元集,则$F=(y\vee g_1)\wedge\cdots\wedge(y\vee g_p)\wedge(\lnot y\vee h_1)\wedge\cdots\wedge(\lnot y\vee h_q)$为合取范式,与$E$有相同的可满足性,其中$y$为新变元
1SAT和2SAT有线性时间算法,但3合取范式的可满足性问题(3SAT)是NP完全问题。为此把CSAT多项式归约到3SAT(3SAT当然是NP的),这只用把各合取项相应地替换(新的项与原来项可满足性相同,而且原来的成真指派为新的成真指派的限制):
- 文字$x$换成$(x\vee y\vee z)\wedge(x\vee y\vee\lnot z)\wedge(x\vee\lnot y\vee z)\wedge(x\vee\lnot y\vee\lnot z)$,其中$y,z$为新的变元
- 文字$x\vee y$换成$(x\vee y\vee z)\wedge(x\vee y\vee\lnot z)$,其中$z$为新的变元
- 文字$x_1\vee\cdots\vee x_m(m>3)$换成$(x_1\vee x_2\vee y_1)\wedge(x_3\vee\lnot y_1\vee y_2)\wedge(x_4\vee\lnot y_2\vee y_3)\wedge\cdots\wedge(x_{m-2}\vee\lnot y_{m-4}\vee y_{m-3})\wedge(x_{m-1}\vee x_m\vee\lnot y_{m-3})$,其中$y_1,\cdots,y_{m-3}$为新的变元。
给定一个无向图$G=(V,E)$,$A\subseteq V$为独立集是指其中任何两点之间没有边,其中顶点数最大的独立集称为$G$的一个最大独立集。独立集问题(IS)问题问一个无向图$G$的最大独立集中顶点数是否大于等于给定的整数$k$。IS问题显然是NP的(可猜测$k$个顶点),我们下面把3SAT多项式归约到IS,给定3合取范式$F=\bigwedge^n_{i=1}\bigvee^3_{j=1}x_{ij}$,构造图$G=(V,E)$,其中$V=\{(i,j)\vert i=1,\cdots,n,j=1,\cdots,3\}$,$E=\{((i,j),(i,k))\vert i=1,\cdots,n,j,k=1,\cdots,3,j\neq k\}\cup\{((i,k),(j,l))\vert i,j=1,\cdots,n,k,l=1,\cdots,3,x_{ik},x_{jl}\text{是相反的文字}\}$,则合取范式$F$可满足当且仅当图$G$最大独立集中顶点数是否大于等于$n$,实际上每个最大独立集对应一种取值方式($(i,j)$在其中则让$x_{ij}$为真)。
顶点覆盖问题问无向图$G=(V,E)$是否存在不超过$k$个顶点的覆盖。它明显是NP的,以下把IS归约为这问题,事实上$G$有大小为$k$的独立集当且仅当它有大小为$\vert V\vert -k$的顶点覆盖。
有向哈密顿回路问题(DHC)问有向图$G$是否存在哈密顿回路。它明显是NP的,以下把3SAT归约为这问题,给定3合取范式$F=\bigwedge^n_{i=1}\bigvee^3_{j=1}x_{ij}$:
- 对每个变元$x_i$构造子图$H_i$如图a,其中$m_i$为$x_i$与$\lnot x_i$中在$F$出现次数的较大者,再把这些子图如图b连接成图$H$。注意对这图的哈密顿回路,从$a_i$开始,只有$a_i,b_{i0},c_{i1},\cdots,b_{im_i},c_{im_i},d_i;a_i,c_{i0},b_{i1},\cdots,c_{im_i},b_{im_i},d_i$两种选择,我们将用它们分别表示$x_i$为真和假的情况,进而图$H$的哈密顿回路对应于变元的指派。
- 对每个子句$x_i\bigvee^3_{j=1}x_{ij}$构造子图$I_i$如图c,注意若哈密顿回路从$r_i,s_i,t_i$进入则必相应从$u_i,v_i,w_i$离开。接着,
- 若$x_{i,1}=x_k$,则把某个未这样用过的$c_{kp}$连接到$r_i$,又把$u_i$连接到$b_{k,p+1}$,对其余两个变元类似处理
- 若$x_{i,1}=\lnot x_k$,则把某个未这样用过的$b_{kp}$连接到$r_i$,又把$u_i$连接到$c_{k,p+1}$,对其余两个变元类似处理
现在$F$的成真指派对应于图的哈密顿回路。
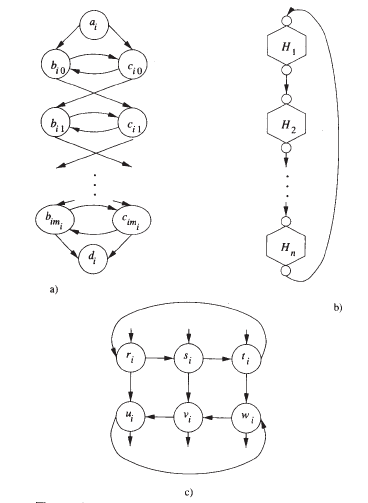
无向哈密顿回路问题(HC)问无向图$G$是否存在哈密顿回路。它明显是NP的,以下把DHC归约为这问题,给定有向图$G=(V,E)$,令$V’=V\times\{0,1,2\}$,$E’=\{((v,i),(v,i+1))\vert v\in V,i=0,1\}\cup\{((v,2),(w,0))\vert (v,w)\in E\}$,则无向图$G’=(V’,E’)$有哈密顿回路当且仅当$G$有哈密顿回路。
货郞问题(TSP)问边带整数权的无向图$G$是否存在总权不超过$k$的哈密顿回路。它明显是NP的,以下把HC归约为这问题,事实上只用为每条边给权1,则原图有哈密顿回路当且仅当带权图有权不超过顶点数的哈密顿回路。
子集和问题问一个给定的正整数集是否存在一个子集中各数之和为一个给定整数。它明显是NP的,以下把3SAT归约为这问题,给定3合取范式$F=\bigwedge^n_{i=1}\bigvee^3_{j=1}X_{ij}$,其中变元个数为$m$,构造8进制表示如下的各整数组成的集合:
| 记号 | 位1 | 位2 | …… | 位m | 位m+1 | …… | 位m+n |
|---|---|---|---|---|---|---|---|
| $y_1$ | 1 | 0 | 0 | $\alpha_{1,1}$ | $\alpha_{n,1}$ | ||
| $z_1$ | 1 | 0 | 0 | $\beta_{1,1}$ | $\beta_{n,1}$ | ||
| $y_2$ | 0 | 1 | 0 | $\alpha_{1,2}$ | $\alpha_{n,2}$ | ||
| $z_2$ | 0 | 1 | 0 | $\beta_{1,2}$ | $\beta_{n,2}$ | ||
| …… | …… | …… | …… | …… | …… | …… | …… |
| $y_m$ | 0 | 0 | 1 | $\alpha_{1,m}$ | $\alpha_{n,m}$ | ||
| $z_m$ | 0 | 0 | 1 | $\beta_{1,m}$ | $\beta_{n,m}$ | ||
| $g_1$ | 0 | 0 | 0 | 1 | 0 | ||
| $h_1$ | 0 | 0 | 0 | 1 | 0 | ||
| …… | …… | …… | …… | …… | …… | …… | …… |
| $g_n$ | 0 | 0 | 0 | 0 | 1 | ||
| $h_n$ | 0 | 0 | 0 | 0 | 1 |
其中$\alpha_{ij}$在某$X_{ik}$为第$j$个变元时为1,否则0;$\beta_{ij}$在某$X_{ik}$为第$j$个变元否定时为1,否则0。考虑它大小按8进制为$\stackrel{m}{\overbrace{11\cdots 1}}\stackrel{n}{\overbrace{33\cdots 3}}$的子集,则对每个$i$,$y_i$与$z_i$有且只有一个在其中,分别对应第$i$个变元为真或假。这样,存在上述子集当且仅当$F$可满足。
虽然P问题的补是P问题,但NP问题的补不一定是NP问题,由NP补问题组成的问题类记为$co-\mathcal{NP}$。注意到$\mathcal{NP}=co-\mathcal{NP}$当且仅当某个NP完全问题的补为NP问题。由于人们猜测NP完全问题SAT的补不是NP的,这两个问题类可能不同。
其它问题类
前面我们关心的问题类都以多项式为界,在此以后最重要的指数函数和对数函数。这里不打算讨论这些让人目不暇给的结果,如非确定性对数空间问题类与补非确定性对数空间问题类相同。我们给出用于判断两个问题类不同的一个相当一般的结果。
设$f:\mathbb{N}\to\mathbb{N}, f(n)\geq\log n$,若存在空间复杂度$O(f)$的算法把$1^n$映射到$f(n)$的二进制表示,则称$f$为空间可构造的。空间层次定理断言,对任何空间可构造函数$f$存在语言$A$,使存在空间复杂度$O(f)$的算法判定它,但不存在空间复杂度$o(f)$的算法判定它。常见的函数多为空间可构造的,作为推论,多项式空间问题类真包含于指数空间问题类,而且对正数$\alpha_1<\alpha_2$,存在$O(n^{\alpha_2})$空间问题不是$O(n^{\alpha_1})$空间问题。
为论证空间层次定理,我们构造一个算法$B$,对于输入$w$:
- 令$n=\vert w\vert $
- 计算$f(n)$并划分出这么多带空间,后面如果越界使用则拒绝
- 若$w$不形如$<M>10^\ast $,其中$<M>$为一图灵机的描述,则拒绝
- 对$w$模拟运行$M$最多$2^{f(n)}$步(这只须设立一个$f(n)$位计数器)
- 若$M$接受则拒绝,否则接受
$B$显然只用$O(f)$空间,而若有空间复杂度$g=o(f)$的算法$M$也判定$B$的语言,则对输入$<M>10^m$($m$充分大),$M$将在$2^{dg(n)}\leq 2^{f(n)}$步内完成,从而$M$与$B$中刚好有一个接受$w$,与$M$的定义矛盾。
类似地,设$f:\mathbb{N}\to\mathbb{N}, f(n)\geq n\log n$,若存在时间复杂度$O(f)$的算法把$1^n$映射到$f(n)$的二进制表示,则称$f$为时间可构造的。时间定理层次断言,对任何时间可构造函数$f$存在语言$A$,使存在时间复杂度$O(f)$的算法判定它,但不存在时间复杂度$o(\frac{f}{\log f})$的算法判定它。常见的函数多为时间可构造的,作为推论,多项式时间问题类真包含于指数时间问题类(存在$k$使时间复杂度不超过$O(2^{n^k})$),而且对正数$\alpha_1<\alpha_2$,存在$O(n^{\alpha_2})$时间问题不是$O(n^{\alpha_1})$时间问题。
为论证时间层次定理,方法类似,我们构造一个算法$B$,对于输入$w$:
- 令$n=\vert w\vert $
- 计算$\lceil \frac{f(n)}{\log f(n)}\rceil$
- 若$w$不形如$<M>10^\ast $,其中$<M>$为一图灵机的描述,则拒绝
- 对$w$模拟运行$M$最多$\lceil \frac{f(n)}{\log f(n)}\rceil$步
- 若$M$接受则拒绝,否则接受
$B$显然只用$O(f)$时间,而若有时间复杂度$g=o(\frac{f}{\log f})$的算法$M$也判定$B$的语言,则对输入$<M>10^m$($m$充分大),$M$将在$g(n)\leq \lceil \frac{f(n)}{\log f(n)}\rceil$步内完成,从而$M$与$B$中刚好有一个接受$w$,与$M$的定义矛盾。
其实我们可以直接构造一个非多项式时间的问题:广义正则表达式的等价性问题,即两个容许幂运算(设$R$为正则表达式,$k$为整数,则$R^{k}$接受的语言与$\stackrel{k}{\overbrace{RR\cdots R}}$接受的语言相同)的正则表达式是否对应相同的语言。这问题显然有指数时间算法,因为可以把幂运算展开为标准的正则表达式,再用标准的方法。接着证明任何指数时间问题都可多项多归约到这问题,为此给定一个$2^{\vert w\vert ^k}$时间算法$M$和输入串$w=a_1\cdots a_n$,让正则表达式$Q$接受语言$(\Gamma\cup Q\cup \{\#\})^\ast =\Delta ^\ast $,而$R$接受不代表拒绝$w$的瞬时格局序列的串,于是两个广义正则表达式接受相同语言当且仅当$M$接受$w$。现在只用完成$R$的构造,注意到不代表拒绝的瞬时格局序列的串有三种可能性,故令$R=R_s\vert R_e\vert R_n$:
- 开始的瞬时格局不对,对应于$R_s=S_{0,q_0}\vert S_{1,a_1}\vert \cdots\vert S_{n,a_n}\vert S_b\vert S_{2^{n^k},\#}$,其中
- $S_{iX}=\Delta^{i}(\Delta\setminus\{X\})\Delta^\ast $
- $S_b=\Delta^{n+1}(\Delta\vert \epsilon)^{2^{n^k}-n-2}(\Delta\setminus\{B\})\Delta^\ast $
- 结束的瞬时格局不对,对应于$R_e=(\Delta\setminus(Q\setminus F))^\ast $
- 中间的转移错误,对应于$R_n=\bigvee_{abc\text{不会转换成}def}\Delta ^\ast abc\Delta^{2^{n^k}-2}xyz\Delta ^\ast $
带谕示的图灵机
语言L的谕示就是一个能报告任何一个串是否属于语言L的装置,带谕示的图灵机是一台多带图灵机,按转移函数应向第二条带(谕示带)写入一个特殊符号后实际写到带上是原来这带上的串是否属于语言L。若一台带语言B谕示的图灵机接受的语言为A,则称A可图灵归约到B。显然,映射可归约是图灵可归约的特殊情况。
这个概念广泛到有点玄(因为假设存在似乎不存在的东西),例如
- 带一个NP完全问题谕示的图灵机可以在多项式时间内判定所有NP问题和NP补问题
- 带停机问题谕示的图灵机可以判定上述的不可判定问题(但利用对角线方法仍然有它们无法判定的问题)。
给定语言L的谕示,把带谕示L的图灵机能在确定性和非确定性多项式时间内可判定的问题类记作$\mathcal{P}^L$和$\mathcal{NP}^L$。
- 存在谕示$A$使$\mathcal{N}^A\neq\mathcal{NP}^A$,考虑语言$L_A=\{w\vert \exists x\in A(\vert x\vert =\vert w\vert )\}$,则$L_A\in\mathcal{NP}^A$,记$M_1,\cdots$为所有谕示图灵机,不妨设$M_i$时间复杂度不超过$n^i$,对每个i 取$n$比所有已决定归属的串长度大且$2^n>n^i$,对$1^n$运行$M_i$,其中谕示回答属于当且仅当询问的串已确定属于$A$,若它接受则让串不属于$A$,反之亦然。 这样,$M^A_i$接受$1^n$当且仅当$1^n\notin L_A$,结果没有多项式时间的图灵机能判定$L_A$。
- 存在谕示$B$使$\mathcal{N}^B=\mathcal{NP}^B$,取$B$为一个NS完全问题即有$\mathcal{NP}^B\subseteq\mathcal{NS}=\mathcal{S}\subseteq\mathcal{P}^B$
因对角线方法可用于带谕示的图灵机,这表明用对角线方法去证明$\mathcal{N}\neq\mathcal{NP}$是没什么希望的。
随机化图灵机
前述图灵机对于相同输入串总得到相同结果。随机化图灵机可视为一台多带图灵机,其中第二条带(随机带)所有格子分别初始化为0或1,可视为由位组成。这样,对每个输入串,可以按所有可能的随机带平均定义它被随机化图灵机接受的概率。
设L为一个语言,若存在蒙特卡罗随机化算法M:
- 对非L中的串,M接受它的概率为0
- 对L中的串,M接受它的概率至少为$\frac{1}{2}$(其实以为0与1间的其它数也一样)
- M的时间复杂度不超过输入长度的多项式,与随机带无关
则称L为随机多项式的问题,随机多项式的问题组成问题类$\mathcal{RP}$。通过猜测随机位可知$\mathcal{RP}\subseteq\mathcal{NP}$。这样的例子有基于费马小定理的合数判断。通过重复运行随机化算法,可以得到没有取伪错误而出现弃真错误概率任意小的算法。
原则上还可以考虑取伪错误和弃真错误都可能出现的情况,如通过随机行走判断两个分支程序是否等价,但这里不展开。
设L为一个语言,若存在拉斯维加斯随机化算法M:
- M接受语言L
- M的时间复杂度按随机带平均不超过输入长度的某个多项式
则称L为零错误概率多项式的问题,随机多项式的问题组成问题类$\mathcal{ZPP}$。显然$\mathcal{P}\subseteq\mathcal{ZPP}$。
我们指出$\mathcal{ZPP}=\mathcal{RP}\cap co-\mathcal{RP}$,
- 给定语言L拉斯维加斯算法M,平均时间复杂度不超过多项式$p$,我们可以构造蒙特卡罗算法模拟M的$2p(\text{输入长度})$步,若期间进入接受状态则接受,否则拒绝。易见,它不会接受非L的串(因M不会)且是多项式时间的,对L中的串也会以至少$\frac{1}{2}$概率接受(否则M的平均时间复杂度大于$\frac{1}{2}2p=p$)。对L的补也可类似构造。
- 给定语言L和其补的蒙特卡罗算法$M$和$M’$,则构造拉斯维加斯算法运行它们,若前者接受则接受,若后者接受则拒绝,其它情况则重复。因为一轮中得出结果的概率至少$\frac{1}{2}$,所以轮数期望为$\sum^{\infty}_{i=1}\frac{i}{2^i}<+\infty$。
其它
存在不借助图灵机而讲述可计算函数的等价理论,部分递归函数是一种:
一个原始递归函数可由以下规则构造得到:
- 零函数$f:\mathbb{N}\to\mathbb{N}, x\mapsto 0$和后继函数$g:\mathbb{N}\to\mathbb{N}, x\mapsto x+1$是原始递归函数
- 若$f:\mathbb{N}^n\to\mathbb{N}$是原始递归函数,$e_1,\cdots,e_n\in\mathbb{N}$,则代入函数$g:\mathbb{N}^n\to\mathbb{N}, x\mapsto f(e_1,\cdots,e_n)$是原始递归函数
- 若$f:\mathbb{N}^k\to\mathbb{N}, g_i:\mathbb{N}^n\to\mathbb{N}$是原始递归函数,则复合函数$h:\mathbb{N}^n\to\mathbb{N}, x\mapsto f(g_1(x),\cdots,g_k(x))$是原始递归函数
- 若$f:\mathbb{N}^n\to\mathbb{N},g:\mathbb{N}^{n+2}\to\mathbb{N}$是原始递归函数,则原始递归函数$h:\mathbb{N}^{n+1}\to\mathbb{N}, (0,x)\mapsto f(x), (t+1,x)\mapsto g(t,h(t,x),x)$是原始递归函数
一个部分递归函数可由以下规则构造得到(只有最后一条是新的):
- 零函数$f:\mathbb{N}\to\mathbb{N}, x\mapsto 0$和后继函数$g:\mathbb{N}\to\mathbb{N}, x\mapsto x+1$是部分递归函数
- 若$f:\mathbb{N}^n\to\mathbb{N}$是原始递归函数,$e_1,\cdots,e_n\in\mathbb{N}$,则代入函数$g:\mathbb{N}^n\to\mathbb{N}, x\mapsto f(e_1,\cdots,e_n)$是部分递归函数
- 若$f:\mathbb{N}^k\to\mathbb{N}, g_i:\mathbb{N}^n\to\mathbb{N}$是原始递归函数,则复合函数$h:\mathbb{N}^n\to\mathbb{N}, x\mapsto f(g_1(x),\cdots,g_k(x))$是部分递归函数
- 若$f:\mathbb{N}^n\to\mathbb{N},g:\mathbb{N}^{n+2}\to\mathbb{N}$是原始递归函数,则原始递归函数$h:\mathbb{N}^{n+1}\to\mathbb{N}, (0,x)\mapsto f(x), (t+1,x)\mapsto g(t,h(t,x),x)$是部分递归函数
- 若$f:\mathbb{N}^{n+1}\to\mathbb{N}$是原始递归函数,则原始递归函数$h:\mathbb{N}^n\to\mathbb{N}, x\mapsto \inf\{t\in\mathbb{N}\vert f(t,x)=0\}$是部分递归函数
这种描述方案更为接近数论,但整数似乎往往不及文本好用。